两端固定的纸张拱起所成曲线的方程是什么？

既不是正态分布也不是悬链线、抛物线，准确的说角度在弧长参数下解的形式是椭圆函数，还需要通过曲线论基本定理映射回Descartes坐标系。结果如下：分子动力学结果概述这个问题可以简化为二维平面的弹性曲线。一般情况是Euler弹性线问题，简单的说就是仅仅考虑弯曲能情况下，一条曲线两端在位移和角度的约束下能量最小的构型是什么？人们在1800s左右已经意识到这个问题与单摆的相似性。【4】考虑Kirchhoff杆的静态情况下的控制方程如下：具体含义是杆内力的线密度与力载荷平衡，内力矩的线密度与杆弯曲时内力对矩的贡献以及矩载荷平衡。具体推导可以参考如何理解Kirchhoff弹性杆？化简取以杆长为参数的自然坐标系(Frenet标架)，把外载荷以及轴力在Frenet标架上展开，得到二维弹性杆方程的分量形式（具体可以参考弹性杆理论的简化形式）：如果载荷仅仅分布在两端，载荷可以作为边界条件处理。载荷一般分为死载（dead load）以及活载（live load）。死载就是方向与弹性杆几何无关的载荷，比如说拱纸过程中两侧一直朝着中心运动，可以看作死载。活载比如说静水压，是沿着杆的几何构型分布的，一般来说死载求解涉及到参考标架到随体标架的变换（通过欧拉角或者四元数或者罗德里格斯公式之类的），求解比较复杂，但是当载荷仅仅分布在边界的时候，可以作为边界条件处理，弹性杆方程会化简为一个相对简单的形式。载荷形式如下（δ函数可以用来表示集中力和力矩，这个在用mathematica实现剪力图和弯矩图的绘制中求解小变形梁挠度曲线的解析形式中由很大作用。）：对弹性杆方程的分量形式积分，并带入边界载荷，得到：其中，。端部力矩：可以看出以上微分方程其实就是单摆方程，解可以通过椭圆函数形式表达，自然科学中确定性问题的应用数学中给出了单摆的一些渐近级数解。分析两边拱起，边界条件可以表示为。只要通过这个边界条件对微分方程打靶即可。但是实际操作中会出现很多问题，这种非线性方程对打靶的初值要求比较高，方程存在很多解，但是满足实际的解只有一个。想要求解得到实际中的图形，就必需对解进行估计。（感觉matlab内置函数bvp4c；bvp5c厉害的一点就是一般我们打靶过程中给定的都是初值，但是通过这个函数我们可以直接给出对解的估计，理论上说数值稳定性更高了。）纸张拱起时，两端角度为0，中间也为0，因此可以选择如下估计函数：然后通过不断改变P的值，就可以得到图1中不同形式的解。类似的有很多相关研究可以参考。验证这个问题无论是分子动力学还是实际都可以很容易的验证。代码代码放在下面需要可以自取。matlab%% EulerRod2D %% 赋值 clear;clc; Pa=0; Pb=5; phi=atan2(Pb,Pa); l=50;EI=5000;M0=0;M1=0; N=2000; M0p=M0/(EI/l); M1p=M1/(EI/l); Pap=Pa/(EI/l^2); Pbp=Pb/(EI/l^2); Pp=sqrt(Pap^2+Pbp^2); mm0=M0p; % 起始约化弯矩 mm1=M1p; % 末态约化弯矩 thetap=zeros(N,2); sp=linspace(0,1,N); %% 计算 % Pp=502.6825; % Pp=39~63 66.5 71; % Pp=72~73 产生自接触问题; % Pp=100~1000之间出现混沌行为！ % Pp=0~38之间不会有解 -50~0之间没有解 -2000~-50之间没有解 Pp=72.2; sep=[45 50 55 60 65 72] for i=6 Pp=sep(i); N=2000; xmesh=linspace(0,1,N); %创建网格 solinit=bvpinit(xmesh,@guess); %创建初始值以及网格 opts = bvpset('FJacobian',@(x,y) jac(x,y,Pp),'RelTol',1e-3,'AbsTol',1e-6,'Stats','on'); sol=bvp5c(@(x,y) bvpfcn(x,y,Pp),@(ya,yb) bcfcn(ya,yb,0,0),solinit,opts) % plot(sol.x,sol.y(1,:)); %% 绘图 % figure(1) % plot(1:length(sol.y(1,:)),sol.y(1,:)+phi); xlabel("s") ylabel("\theta") % figure(2) % plot(1:length(sol.y(1,:)),sol.y(2,:)); xlabel("s") ylabel("\kappa") d0=[1 0;0 1]; r=Frenet2descarte2D(1,sol.y(2,:),d0); figure(3) subplot(2,3,i) if Pp

李芷晴

Apr 19, 2024 - 03:00

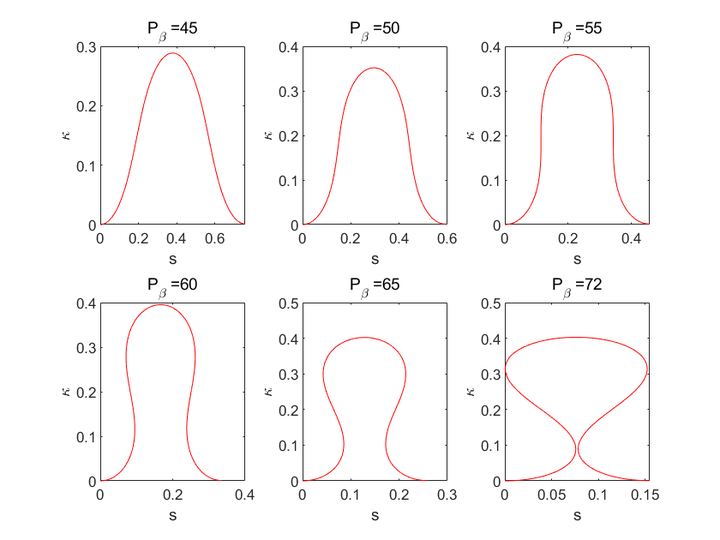
既不是正态分布也不是悬链线、抛物线，准确的说角度在弧长参数下解的形式是椭圆函数，还需要通过曲线论基本定理映射回Descartes坐标系。

结果如下：

分子动力学结果

概述

这个问题可以简化为二维平面的弹性曲线。一般情况是Euler弹性线问题，简单的说就是仅仅考虑弯曲能情况下，一条曲线两端在位移和角度的约束下能量最小的构型是什么？

人们在1800s左右已经意识到这个问题与单摆的相似性。【4】

考虑Kirchhoff杆的静态情况下的控制方程如下：

$\frac{\partial \mathbf{F}}{\partial s}+\boldsymbol{q}=0 \\ \frac{\partial \mathbf{M}}{\partial s}+\frac{\partial \boldsymbol{r}}{\partial s}\times \mathbf{F}+\mathbf{m}=0\\$ 具体含义是杆内力的线密度与力载荷平衡，内力矩的线密度与杆弯曲时内力对矩的贡献以及矩载荷平衡。具体推导可以参考如何理解Kirchhoff弹性杆？

化简

取以杆长为参数的自然坐标系(Frenet标架)，把外载荷以及轴力在Frenet标架上展开，得到二维弹性杆方程的分量形式（具体可以参考弹性杆理论的简化形式）：

$\begin{cases} \left( \mathrm{F}_1\mathbf{d}_1+\mathrm{F}_2\mathbf{d}_2 \right) '+\rm \boldsymbol q\left( s \right) =0\\ \mathrm{M}'+\mathrm{F}_2+\mathrm{m}=0\\ \end{cases}$

如果载荷仅仅分布在两端，载荷可以作为边界条件处理。

载荷一般分为死载（dead load）以及活载（live load）。

死载就是方向与弹性杆几何无关的载荷，比如说拱纸过程中两侧一直朝着中心运动，可以看作死载。

活载比如说静水压，是沿着杆的几何构型分布的，一般来说死载求解涉及到参考标架到随体标架的变换（通过欧拉角或者四元数或者罗德里格斯公式之类的），求解比较复杂，但是当载荷仅仅分布在边界的时候，可以作为边界条件处理，弹性杆方程会化简为一个相对简单的形式。

载荷形式如下（δ函数可以用来表示集中力和力矩，这个在用mathematica实现剪力图和弯矩图的绘制中求解小变形梁挠度曲线的解析形式中由很大作用。）：

$\begin{cases} \mathbf{P}\left( s \right) =\mathbf{P}_0+\mathbf{P}_1=\left( \mathrm{P}_{\alpha}\mathbf{i}+\mathrm{P}_{\beta}\mathbf{j} \right) |_{s=0}-\left( \mathrm{P}_{\alpha}\mathbf{i}+\mathrm{P}_{\beta}\mathbf{j} \right) |_{s=1}=\mathbf{i}\int_0^s{\left( \delta \left( x \right) -\delta \left( l-x \right) \right) \mathrm{P}_{\alpha}dx}+\mathbf{j}\int_0^s{\left( \delta \left( x \right) -\delta \left( l-x \right) \right) \mathrm{P}_{\beta}dx}\\ \mathbf{M}\left( s \right) =\mathbf{M}_0+\mathbf{M}_1=\int_0^s{\delta \left( x \right) \mathbf{M}_0+\delta \left( l-x \right) \mathbf{M}_1dx}\\ q\left( s \right) =\left( \delta \left( s \right) -\delta \left( l-s \right) \right) \mathrm{P}_{\alpha}\mathbf{i}+\left( \delta \left( s \right) -\delta \left( l-s \right) \right) \mathrm{P}_{\beta}\mathbf{j}=\frac{d\mathbf{P}\left( s \right)}{ds}\\ m\left( s \right) =\delta \left( s \right) \mathbf{M}_0+\delta \left( l-s \right) \mathbf{M}_1=\frac{d\mathbf{M}\left( s \right)}{ds}\\ \end{cases}$

对弹性杆方程的分量形式积分，并带入边界载荷，得到：

$\begin{cases} \mathrm{F}_1=-\left( \mathrm{P}_{\alpha}\cos \theta +\mathrm{P}_{\beta}\sin \theta \right)\\ \mathrm{F}_2=\mathrm{P}_{\alpha}\sin \theta -\mathrm{P}_{\beta}\cos \theta\\ \Theta ''\left( \bar{s} \right) +\bar{\mathrm{P}}\sin \Theta \left( \bar{s} \right) =0\\ \end{cases}$

其中， $\tan \varphi =\frac{\mathrm{P}_{\alpha}}{\mathrm{P}_{\beta}}, \bar{\mathrm{P}}=\frac{\sqrt{{\mathrm{P}_{\alpha}}^2+{\mathrm{P}_{\beta}}^2}}{\mathrm{EI}/l^2}, \bar{s}=\frac{s}{l}, \Theta =\theta \left( \bar{s} \right) -\varphi, \bar{\mathrm{M}}_0=\frac{\mathrm{M}_0}{\mathrm{EI}/l},\bar{\mathrm{M}}_1=\frac{\mathrm{M}_1}{\mathrm{EI}/l}$ 。

端部力矩：

$\begin{cases} \Theta '\left( 0 \right) =\bar{\mathrm{M}}_0\\ \Theta '\left( 1 \right) =\bar{\mathrm{M}}_1\\ \end{cases}$

可以看出以上微分方程其实就是单摆方程，解可以通过椭圆函数形式表达，

自然科学中确定性问题的应用数学中给出了单摆的一些渐近级数解。

分析

两边拱起，边界条件可以表示为 $\theta(0)=0; \theta(1)=0$ 。

只要通过这个边界条件对微分方程打靶即可。

但是实际操作中会出现很多问题，这种非线性方程对打靶的初值要求比较高，方程存在很多解，但是满足实际的解只有一个。

想要求解得到实际中的图形，就必需对解进行估计。（感觉matlab内置函数bvp4c；bvp5c厉害的一点就是一般我们打靶过程中给定的都是初值，但是通过这个函数我们可以直接给出对解的估计，理论上说数值稳定性更高了。）

纸张拱起时，两端角度为0，中间也为0，因此可以选择如下估计函数：

$\begin{cases} \theta ^*\left( s \right) =\sin \left( 2\pi s \right)\\ {\theta ^*}^{(1)}\left( s \right) =2\pi \cos \left( 2\pi s \right)\\ \end{cases}$

然后通过不断改变P的值，就可以得到图1中不同形式的解。

类似的有很多相关研究可以参考。

验证

这个问题无论是分子动力学还是实际都可以很容易的验证。

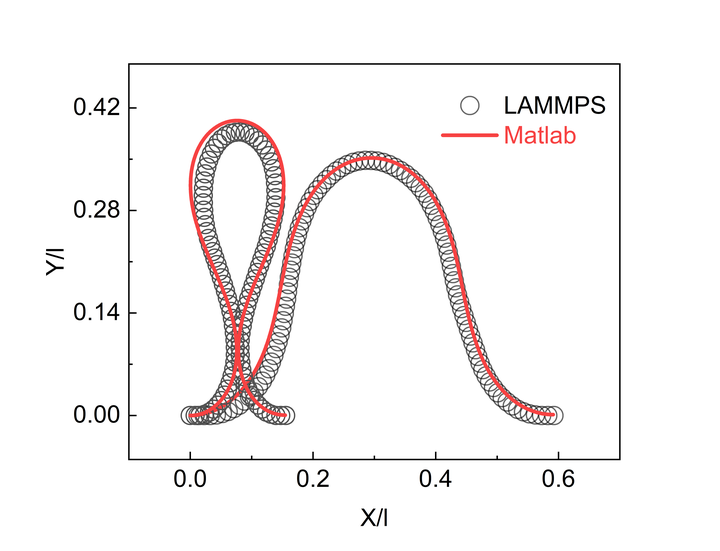
代码

代码放在下面需要可以自取。

matlab

%% EulerRod2D
%% 赋值
clear;clc;
Pa=0;
Pb=5;
phi=atan2(Pb,Pa);
l=50;EI=5000;M0=0;M1=0;
N=2000;
M0p=M0/(EI/l);
M1p=M1/(EI/l);
Pap=Pa/(EI/l^2);
Pbp=Pb/(EI/l^2);
Pp=sqrt(Pap^2+Pbp^2);
mm0=M0p; % 起始约化弯矩
mm1=M1p; % 末态约化弯矩
 
thetap=zeros(N,2);
sp=linspace(0,1,N);
%% 计算
% Pp=502.6825;
% Pp=39~63 66.5 71;
% Pp=72~73 产生自接触问题;
% Pp=100~1000之间出现混沌行为！
% Pp=0~38之间不会有解 -50~0之间没有解 -2000~-50之间没有解
Pp=72.2;
sep=[45 50 55 60 65 72]
for i=6
Pp=sep(i);
N=2000;
xmesh=linspace(0,1,N); %创建网格
solinit=bvpinit(xmesh,@guess); %创建初始值以及网格
opts = bvpset('FJacobian',@(x,y) jac(x,y,Pp),'RelTol',1e-3,'AbsTol',1e-6,'Stats','on');
sol=bvp5c(@(x,y) bvpfcn(x,y,Pp),@(ya,yb) bcfcn(ya,yb,0,0),solinit,opts)
% plot(sol.x,sol.y(1,:));

%% 绘图
% figure(1)
% plot(1:length(sol.y(1,:)),sol.y(1,:)+phi);
xlabel("s")
ylabel("\theta")
% figure(2)
% plot(1:length(sol.y(1,:)),sol.y(2,:));
xlabel("s")
ylabel("\kappa")

d0=[1 0;0 1];
r=Frenet2descarte2D(1,sol.y(2,:),d0);
figure(3)
subplot(2,3,i)
if Pp<58
plot(r(:,1),r(:,2),"r-")
else
plot(r(:,1),-r(:,2),"r-")   
hold on
end
title(strcat("P_\beta =",num2str(sep(i))))
end
%% 函数

function dydx = bvpfcn(x,y,p)
dydx = zeros(2,1);
dydx = [y(2) 
    -p*sin(y(1))];
end
function res = bcfcn(ya,yb,m0,m1)
res = [ya(1)-m0 yb(1)-m1];
end
function g=guess(x)
g= [sin(2*pi*x) 2*pi*cos(2*pi*x)];
end
function dfdy = jac(x,y,p)
dfdy = [0      1
       -p*cos(y(1)) 0];
end

Frenet2Descarte2D.m

%% Frenet2descarte2D
function r=Frenet2descarte2D(sc,kc,d0)
s=sc;
N=length(kc);
d10=d0(1,:);
d20=d0(2,:);
ds=s/N;
coord=zeros(N,2,2);
coord(1,:,1)=d10;
coord(1,:,2)=d20;
% 定义转换矩阵
GAMMA=zeros(2,2,N);
GAMMA(1,2,:)=kc;
GAMMA(2,1,:)=-kc;
con1=GAMMA*ds;con2=-GAMMA*ds;
con1=2*teye(2,N)+con1;
con2=2*teye(2,N)+con2;
teye(2,3)
con=pagemtimes(con1,pageinv(con2));
r=zeros(N+1,2);
r(1,:)=[0 0];
for i=1:N
    coord(i+1,:,1) =con(1,1,i)*coord(i,:,1)+con(1,2,i)*coord(i,:,2);
    coord(i+1,:,2)=con(2,1,i)*coord(i,:,1)+con(2,2,i)*coord(i,:,2);
end
for i=1:N
    r(i+1,:)=r(i,:)+(coord(i,:,1)+coord(i+1,:,1))/2*ds;
end
end

teye.m

function y=teye(a,b)
tem=zeros(a,a,b);
for i=1:a
    tem(i,i,1:b)=1;
end
y=tem;
end

分子动力学

LAMMPS

# 2d rod bulking
dimension	3
boundary	f f f
atom_style	full
units real
timestep 1.0
neighbor	0.3 bin
neigh_modify	delay 5
# create geometry
pair_style	lj/cut 2.5
bond_style harmonic
angle_style harmonic 
read_data test.data

group left id 1 2 3
group right id  99 100 101 
group mid id 51 
group p id 25
group q id 76
displace_atoms p move 0 1 0 units box
displace_atoms q move 0 -1 0 units box

velocity right set 0.0 0.0 0.0
fix		fl right setforce 0.0 0.0 0.0
fix     1 all nve
fix		2 left move linear 0.000001 0.0 0.0 units box 
thermo		200000
dump		1 all atom 2000 rod.xyz
run		20000000

欧拉弹性线方程与单摆方程的等价性，后面有机会写一写。

---------------------------------------------20230810--------------------------------------------

贴一个Auto07p的求解结果：

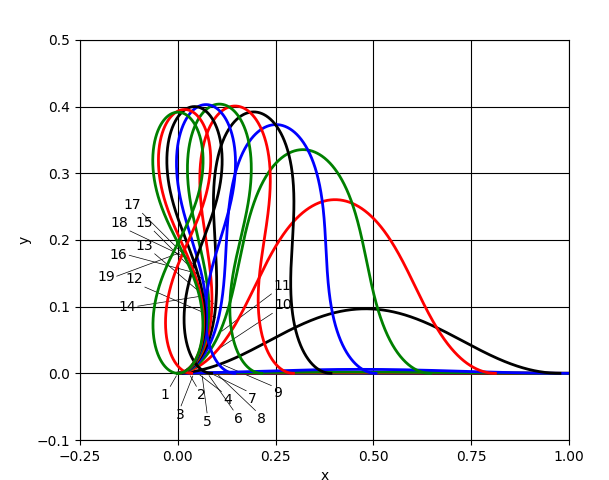
纸张很长的时候，在屈曲较大时还可能出现多个周期的情况：

【参考文献】

【1】Phys. Rev. Lett. 103, 174302
【2】Phys. Rev. Lett. 103, 174301
【3】Volume 5,December 2015, Pages 81-87
【4】Modeling Nonlinear Problems in the Mechanics of Strings and Rods