见证者中的数学原理
起因这些天重新游玩很久之前玩过的游戏《见证者》,回想当初游玩时的兴奋感,依然仿佛历历在目。这个游戏很难称为游戏,而应该看作杰出的艺术品,幻想与写实,表面与暗藏,艺术与数学,精确与诗意,可以谈的东西有很多。这一篇文章就先关注其中蕴含的数学原理。在解谜游戏中,主要的玩法为隐藏物的收集与触发,以及各种有趣的小游戏,益智关卡。在这款游戏中,解密都是通过图中的路径实现的,这就是最形象的图论知识教学。接下来就让我带领大家一一欣赏其中的数学原理。游戏图片来源于网络。内容图论,路径与联通分支简单图,两个顶点,一条边,圆为起点,半圆为终点,看上去就像一个温度计。这幅图,给出的是两点连通性,其中要求每一条边和顶点只可经过一次,这个限制其实相当严苛,所谓的连通就是经由一条又一条边连接,视觉上就是一个连续的道路,也可称为道路联通或者边联通。其实,我们还可以换一个角度理解这个图,对图的划分,我们可以发现黄色的道路把黑色部分分为三块,左,右上和右下,假如我们把黄色道路删掉,留下来的就是三个不联通的部分图,这就是联通分支的概念,每一个子图联通,但是整体不联通,那么这些不联通子图的个数就是联通分支数。很多人学习分析一直搞不清楚联通和联通分支,主要是因为分析使用的空间太好了,很少有不联通的情形,换到图上就一目了然了。做个练习,上图黑色部分有几个联通分支,这里需要注意的是顶点的归属问题,可以规定顶点属于黑色部分,于是答案就是5.可以看作这样的图形连接了五条短链的长链,抽象的看就是一个序结构,正好可以和拓扑联系起来。实现一种图上拓扑的结构,基本流程,选择主链,计数联通分支,添加到主链上,形成一种主序和部分序结合的形式,对于序继续定义拓扑,取下封闭集构成主滤子。挑选合适的滤子元素形成拓扑。这种构造方式非常抽象,而且效果其实相当有限,因为我们通过严苛的条件排除了大量的奇异情形。图论的复杂度可见一般,即使是简单的图,想要完全搞清楚都非常困难。这个图看起来不明所以,其实是添加了经过特定边的约束条件,只不过重合了看不到,比如这幅图,要求经过两个黑点,你会发现很多解法就不能使用了,通过设定条件挑选合适的数学对象,也是常用的手段,比如营业时间,准入标准,候选者资格之类,条件越多满足的人就越少。然后是这个图,颜色块的区分可以看作一种区域界定的作用,路径可以划分出多个分支,这些分支需要容纳单色对象,于是路径的选择就被约束了。我们也可以看到图形由简单到复杂, ,路径越来越复杂。这里其实蕴含着有趣的问题,对于任意满足单经过性的方形图,(就是之前提到的,边,顶点只能经过一次,简称为单经过性),最大的联通分支数是多少?可以视为一个组合图论问题,这样的问题看起来容易,做起来难,可以考虑一个特例, 型图。如图所示,起点终点为两个对角的情况下,联通分支数与n相同。他可以看作一种基本生成模式。由于单经过性,中间需要隔一层,可以发现一些特征,这样的图需要与边界配合才能实现区域划分,因为图形自身不能相交,形不成封闭区域。这也启发了我们玩游戏的时候就要合理的利用边界,边界才是看不见的线。以这个图为例,围成的封闭区域必须与边界相接如红线所示,两个分支均与边界相连。这也是数学有趣的地方,很多看似抽象的条件可以被简单的图形所表达。对称与群论这一部分图表达的是对称路径的概念,对于正方图而言,每条路径都可以唯一对应到对称路径上,这里使用的是中心对称性,还可以取镜像对称性,旋转对称性之类的。中心对称也可以看作绕中心旋转半个圆,180度。这里所展示的数学现象也很有趣,那就是运动与群论,平移,镜像,旋转属于等距变换,即保持物体内部关系不动,改变其位置与形态。就像物理中的刚体模型一样,通过外在关系刻画,就能完全反映本体的运动。这是镜像对称,也可以称为轴对称。这部分开始展示数学对于自然界的刻画,此处是使用路径的纵向距离刻画物体的高度,数学成为了刻画自然的工具,这也是自然哲学的数学原理所表达的观念,自然以数学形式体现其规律,人们通过发掘其中的奥秘获得对自然的审美。这也是物理学最初的目标,使用数学刻画整个宇宙。树与编码这里反映的是二进制编码,如何描述一个物体的位置,逐层分类,一步步细化,最后就获得了这个物体的编码。这方面就是应用数学的领域了,计算机科学,信号与编码,加密与解密。这也是信息时代最为重要的基础科学。表面与隐藏这一部分反映的是太阳照射下的轨迹,虽然看起来仿佛是艺术表现,实际上也带有数学思想的痕迹,使用特定的手段处理后,即使看起来相同的对象也会表现出不同的行为。比如公理体系下的数学对象,看上去都是一个样子,什么信息都得不到,而通过具体的实例,就会发现其中大有不同,这里的太阳照射就是实际计算,缺乏了这一过程,学到的就是抽象的知识,看起来懂很多,实际上啥也干不了,理论终究需要联系实际,在数学上就是实例与计算。到这里,基本原理就介绍完了,后面的都是一些角度与现象的关系,属于认知领域。影子阻拦影子刻画积木限制联通分支形状颜色的混合声音频率的高低建筑物中的隐藏信息图形传达信息,苯环意味着生命,是一种意象。联通区域划分,两个一组,自由度更大局部与整体位置,部分与全局,每个人在自己的角度只能看到局部的现象,局部最优并不是整体最优,但却是这个人能做到的最好的成绩了。结束总的来说,这个游戏还是很不错的,虽然一些谜题真的很难想,不过,数学问题其实也一样,在各种约束条件下寻求最优的答案。当然,数学与图形不过是载体罢了,这个游戏的用意还要更加深刻,下次我再来分析一下这个游戏真正想要传递的理念,各种录音,视频,还有小岛上奇特的景观,雕塑到底是什么?为什么一个先进而落后的世界没有一个文字。下一篇就要谈一谈其中的哲学意味了。 来源:知乎 www.zhihu.com 作者:半数o阿白 【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载

起因
这些天重新游玩很久之前玩过的游戏《见证者》,回想当初游玩时的兴奋感,依然仿佛历历在目。这个游戏很难称为游戏,而应该看作杰出的艺术品,幻想与写实,表面与暗藏,艺术与数学,精确与诗意,可以谈的东西有很多。
这一篇文章就先关注其中蕴含的数学原理。
在解谜游戏中,主要的玩法为隐藏物的收集与触发,以及各种有趣的小游戏,益智关卡。在这款游戏中,解密都是通过图中的路径实现的,这就是最形象的图论知识教学。
接下来就让我带领大家一一欣赏其中的数学原理。游戏图片来源于网络。
内容
图论,路径与联通分支

简单图,两个顶点,一条边,圆为起点,半圆为终点,看上去就像一个温度计。
这幅图,给出的是两点连通性,其中要求每一条边和顶点只可经过一次,这个限制其实相当严苛,所谓的连通就是经由一条又一条边连接,视觉上就是一个连续的道路,也可称为道路联通或者边联通。
其实,我们还可以换一个角度理解这个图,对图的划分,我们可以发现黄色的道路把黑色部分分为三块,左,右上和右下,假如我们把黄色道路删掉,留下来的就是三个不联通的部分图,这就是联通分支的概念,每一个子图联通,但是整体不联通,那么这些不联通子图的个数就是联通分支数。
很多人学习分析一直搞不清楚联通和联通分支,主要是因为分析使用的空间太好了,很少有不联通的情形,换到图上就一目了然了。
做个练习,上图黑色部分有几个联通分支,这里需要注意的是顶点的归属问题,可以规定顶点属于黑色部分,于是答案就是5.可以看作这样的图形
连接了五条短链的长链,抽象的看就是一个序结构,正好可以和拓扑联系起来。实现一种图上拓扑的结构,基本流程,选择主链,计数联通分支,添加到主链上,形成一种主序和部分序结合的形式,对于序继续定义拓扑,取下封闭集构成主滤子。挑选合适的滤子元素形成拓扑。这种构造方式非常抽象,而且效果其实相当有限,因为我们通过严苛的条件排除了大量的奇异情形。图论的复杂度可见一般,即使是简单的图,想要完全搞清楚都非常困难。
这个图看起来不明所以,其实是添加了经过特定边的约束条件,只不过重合了看不到,
比如这幅图,要求经过两个黑点,你会发现很多解法就不能使用了,通过设定条件挑选合适的数学对象,也是常用的手段,比如营业时间,准入标准,候选者资格之类,条件越多满足的人就越少。
然后是这个图,颜色块的区分可以看作一种区域界定的作用,路径可以划分出多个分支,这些分支需要容纳单色对象,于是路径的选择就被约束了。我们也可以看到图形由简单到复杂, ,路径越来越复杂。这里其实蕴含着有趣的问题,对于任意满足单经过性的方形图,(就是之前提到的,边,顶点只能经过一次,简称为单经过性),最大的联通分支数是多少?可以视为一个组合图论问题,这样的问题看起来容易,做起来难,可以考虑一个特例,
型图。
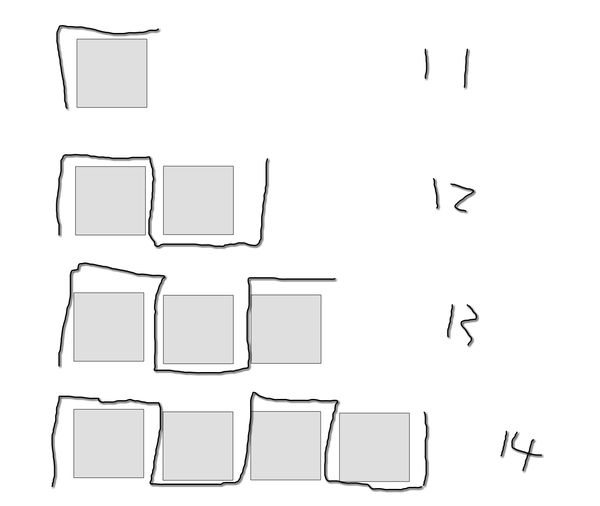
如图所示,起点终点为两个对角的情况下,联通分支数与n相同。他可以看作一种基本生成模式。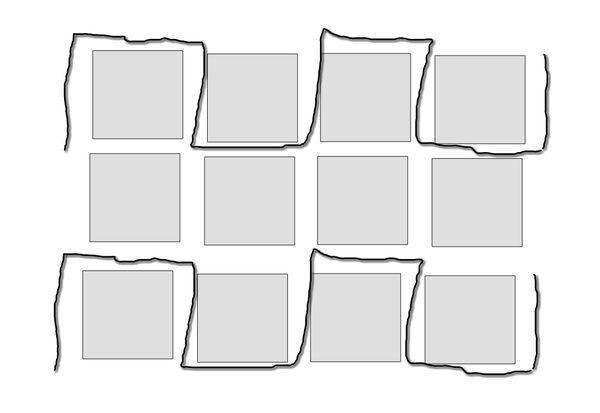
由于单经过性,中间需要隔一层,可以发现一些特征,这样的图需要与边界配合才能实现区域划分,因为图形自身不能相交,形不成封闭区域。这也启发了我们玩游戏的时候就要合理的利用边界,边界才是看不见的线。
以这个图为例,围成的封闭区域必须与边界相接
如红线所示,两个分支均与边界相连。这也是数学有趣的地方,很多看似抽象的条件可以被简单的图形所表达。
对称与群论

这一部分图表达的是对称路径的概念,对于正方图而言,每条路径都可以唯一对应到对称路径上,这里使用的是中心对称性,还可以取镜像对称性,旋转对称性之类的。中心对称也可以看作绕中心旋转半个圆,180度。这里所展示的数学现象也很有趣,那就是运动与群论,平移,镜像,旋转属于等距变换,即保持物体内部关系不动,改变其位置与形态。就像物理中的刚体模型一样,通过外在关系刻画,就能完全反映本体的运动。
这是镜像对称,也可以称为轴对称。
这部分开始展示数学对于自然界的刻画,此处是使用路径的纵向距离刻画物体的高度,数学成为了刻画自然的工具,这也是自然哲学的数学原理所表达的观念,自然以数学形式体现其规律,人们通过发掘其中的奥秘获得对自然的审美。这也是物理学最初的目标,使用数学刻画整个宇宙。
树与编码

这里反映的是二进制编码,如何描述一个物体的位置,逐层分类,一步步细化,最后就获得了这个物体的编码。这方面就是应用数学的领域了,计算机科学,信号与编码,加密与解密。这也是信息时代最为重要的基础科学。
表面与隐藏

这一部分反映的是太阳照射下的轨迹,虽然看起来仿佛是艺术表现,实际上也带有数学思想的痕迹,使用特定的手段处理后,即使看起来相同的对象也会表现出不同的行为。比如公理体系下的数学对象,看上去都是一个样子,什么信息都得不到,而通过具体的实例,就会发现其中大有不同,这里的太阳照射就是实际计算,缺乏了这一过程,学到的就是抽象的知识,看起来懂很多,实际上啥也干不了,理论终究需要联系实际,在数学上就是实例与计算。
到这里,基本原理就介绍完了,后面的都是一些角度与现象的关系,属于认知领域。
影子阻拦
影子刻画
积木限制联通分支形状
颜色的混合
声音频率的高低
建筑物中的隐藏信息
图形传达信息,苯环意味着生命,是一种意象。
联通区域划分,两个一组,自由度更大
局部与整体

位置,部分与全局,每个人在自己的角度只能看到局部的现象,局部最优并不是整体最优,但却是这个人能做到的最好的成绩了。
结束
总的来说,这个游戏还是很不错的,虽然一些谜题真的很难想,不过,数学问题其实也一样,在各种约束条件下寻求最优的答案。当然,数学与图形不过是载体罢了,这个游戏的用意还要更加深刻,下次我再来分析一下这个游戏真正想要传递的理念,各种录音,视频,还有小岛上奇特的景观,雕塑到底是什么?为什么一个先进而落后的世界没有一个文字。下一篇就要谈一谈其中的哲学意味了。
来源:知乎 www.zhihu.com
作者:半数o阿白
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。
点击下载